Why do we need marginalization in BA?

A common practice in Bundle Adjustment is to reduce the state dimension by marginalizing structure or pose states to improve the optimization speed.

In case 3d points(structure) $\textbf{p}_i$ are marginalized out as follows, $\textbf{p}_i$ are triangulated to calculate residual $\textbf{e}$.

where $\textbf{T}_j\in SE(3), \textbf{p}_i\in R^3$ are the states we want to estimate and $\textbf{z}_{ij}$ is the observed feature in $R^2$.

And just optimize the pose related terms only.

Here my question arises. If we can calculate 3d points $\textbf{p}_i$ by the triangulation, only $\textbf{T}_j$ are the state variable to be estimated.

Then, why are we bothered to calculate marginalization related terms $-\textbf{H}_{cs}{\textbf{H}_{ss}}^{-1}\textbf{H}_{sc}$ and $-\textbf{H}_{cs}{\textbf{H}_{ss}}^{-1}\textbf{g}_{s}$ instead of optimizing only poses by ${\textbf{H}}_{cc}\mathbf{\xi}_c ={\textbf{g}}_{c}$ (note that H and g are without bar).

I guess ${\textbf{H}}_{cc}\mathbf{\xi}_c ={\textbf{g}}_{c}$ is enough to find the optimal poses $\textbf{T}_j$.

So, my question was why do we use $\bar{\textbf{H}}_{cc}\mathbf{\xi}_c =\bar{\textbf{g}}_{c}$ instead of ${\textbf{H}}_{cc}\mathbf{\xi}_c ={\textbf{g}}_{c}$?

Answer is simple.

Let’s have a look at the Hessian H of simulated BA.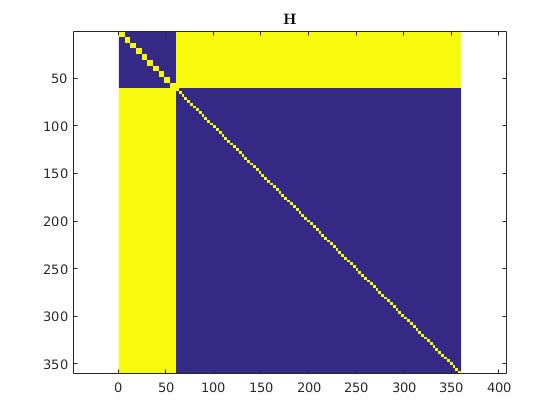

Yello represents non zero element and upper 60 by 60 matrix represent ${\textbf{H}}_{cc}$. When a structure is observed over multiple poses, Hessian make correlation terms.

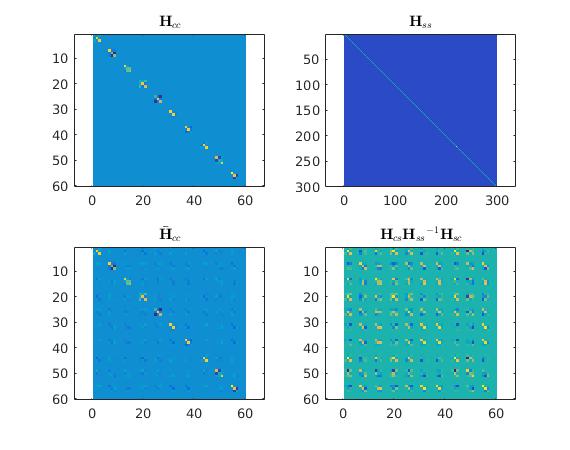
Obiously, ${\textbf{H}}_{cc}\mathbf{\xi}_c ={\textbf{g}}_{c}$ ignores the correlation terms. Therefore, each poses loose information of linkage, whereas in $\bar{\textbf{H}}_{cc}\mathbf{\xi}_c =\bar{\textbf{g}}_{c}$ off diagonal terms are added to Hessian which represents the rumped relationship miginalized from $-\textbf{H}_{cs}{\textbf{H}_{ss}}^{-1}\textbf{H}_{sc}$.

The benefit are faster convergence and low final error in optimization.